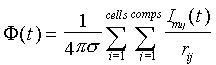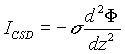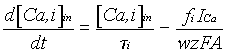Shaping of CA1 Population Spikes



These pages contain a detailed description of the model used in the paper "Macroscopic and Subcellular Factors Shaping Population Spikes" J. Neurophysiol., 83 (4): 2192-2208  by P. Varona, J. M. Ibarz, L. López and O. Herreras (2000). Particularly, the complete Hodgking-Huxley type description of the ionic channels is shown in section 3 and the exact distribution, with values for the maximum conductances and the electrotonic parameters for the different neurons, is depicted in section 7.

This pages should be read along with the paper for a better understanding.
 

Index:

  1. Model of the dorsal CA1 region
  2. Simulation of the field potentials and CSD analysis
  3. CA1 single neuron model:
    1. Soma and dendrite channels
    2. Axon channels
    3. Ca dynamics
    4. Additional notes
  4. Stimuli simulation
  5. Computational methods
  6. Bibliography
  7. Neuron scripts
  8. Contact address


     
     
  1. Model of the dorsal CA1 region 

    2.  

     

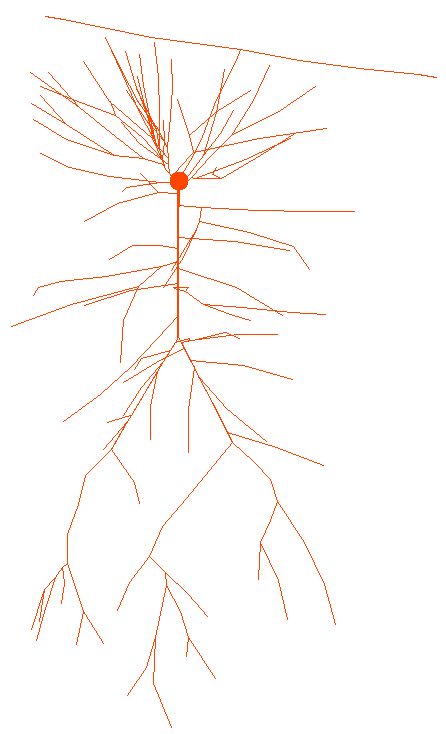
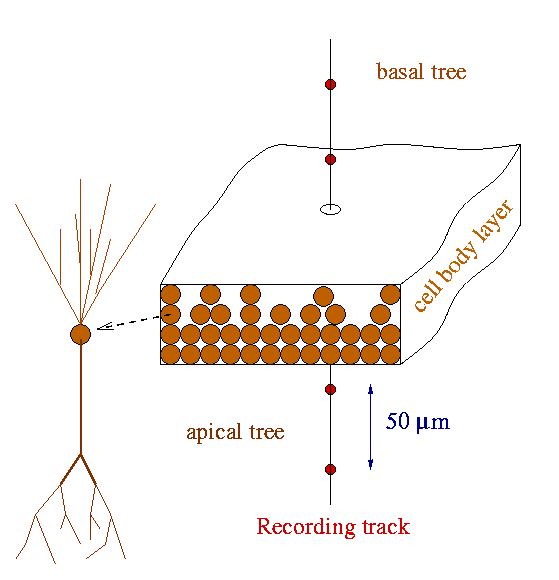
    Our model is built using three levels: supracellular (field potentials and CSDs obtained from the synchronous activity of a population of neurons), cellular (morphology and physiology of the single neurons that make up the ensemble) and subcellular (electrotonic properties, ionic active channels and calcium dynamics for each locus in the morphology). The dorsal CA1 region was modeled with aggregates of different size preserving an experimentally observed cell density of 64 neurons in a 50x50 µm lattice (Boss et al., 1987). The antero-posterior and latero-medial dimensions of the aggregates were 0.05x0.05, 0.2x0.2, 1x0.35, 1x1, and 3x2 mm, corresponding to 64, 1,024, 6,072, 17,424 and 104,544 morphologically identical model neurons, respectively. The dimensions and cell number of the largest aggregate can be taken as a rough estimation for the actual values for the dorsal CA1 region. Three different spatial distribution of neurons were made with their somata arranged either in a monolayer, 4 layers of even density, or a realistic distribution of 4 uneven layers with 66% of somata in the apical side and 22 and 11% in the two layers of the basal side (see schemes in Figure 3 of the paper). Each neuron was rotated a random angle around the somatodendritic axis to test that the particular morphology used in our experiments introduced no artifacts in the field potential calculations. The curvatures in the dorsal CA1 region were neglected for this study.
     
     
     

  2. Simulation of the field potentials and CSD analysis 
     
    A set of 16 recording points 50 µm apart in a vertical track spanning from 250 µm above to 500 µm below the s.p. was placed at the center of the population in parallel to the somatodendritic axis (we termed as b5-b1, s and ap1-ap10 levels, to designate the successive positions at the basal tree, s.p. and apical tree, respectively). The value of field potential measured at each point was calculated as follows:
where sigma is the extracellular conductivity, Imijis the total transmembrane current at the jth compartment of neuron i, and rij is the distance from the recording point to that compartment. Thus, compartments are treated as point sources into a medium of homogeneous conductivity sigma. If the conductivity tensor were known for the CA1 tissue, a more detailed expression could be derived to calculate the field potential with higher accuracy (see Nunez, 1981). These calculations would have a high computational cost due to the presence of complex Bessel functions in the integration of the field potentials. The current density can be obtained (as in the experimental current source density analysis) through a Poisson equation which relates the field potential with the volumetric average of the transmembrane currents:
In a laminated structure such as the CA1 region the overall extracellular currents flow only in the dendrosomatic direction (z axis) and the analysis can be simplified in one dimension:
     
     
     
  1. CA1 single neuron model 

    2.  
2D projection of the 3D morfology2D projection on the x plane
2D projection in the y plane2D projection in the z plane
     

    The prototype model neuron was built with an average dendritic branching pattern, and total dendritic length obtained from detailed morphometric studies (Bannister and Larkman, 1995 a,b; Trommald et al., 1995). The 3D morphology of the neuron was simulated using 265 compartments, distributed in an axon, (consisting of mielinized portions, Ranvier nodes, initial segment and axon hillock), soma and apical and basal dendritic trees (2D projections of the model neuron is shown in the figures above). Total effective area of the neuron was 66,800 microns2 (including spine area).

The electrotonic parameters of the model for the majority of the simulations were Rm=70,000 ohms×cm2, Ri=150 ohm×cm (75 for Results in Figs. 9 and 10), Cm=0.75 microF/cm2. Values of Rm and Cm at the dendritic compartments were compensated to take into account spine area. Input resistance at the soma was 140 Mohms, and tau was 25 ms. See neuron scripts for the exact values of the electrotonic parameters used for each neuron prototype.
CHANNEL DESCRIPTIONS:
1. Soma and dendrite channels:
We used seven ionic channels to simulate the active properties of the somatodendritic membrane: sodium (Na+), calcium (Ca++), and five potassium currents: delayed rectifier (DR), small persistent muscarinic (M), A-type transient (A), short-duration [Ca]- and voltage-dependent (C) and long duration [Ca]-dependent (AHP). Conductance variables were described with Hodgkin-Huxley type formalism. The kinetics of all these channels has been obtained from Warman et al. (1994) with the following modifications: Here we reproduce the description of all channels in the standard Hodgkin-Huxley notation:
Na channel:

INa = gNam3h(Vm-ENa)

ENa = 45 mV

alpham = -3.48(Vm-11.0)/{exp[(Vm-11.0)/-12.94]-1}

betam = 0.12(Vm-5.9)/exp[(Vm-5.9)/4.47]-1}

alphah = 3/exp[(Vm+80)/10]

betah = 12/{exp[(Vm-77)/-27]+1}
 

Ca channel:

ICa = gCas2r(Vm-ECa)

ECa = -13.3Ln([Ca,1]in/1200)

alphas = -0.16(Vm+26.0)/{exp[(Vm+26)/-4.5]-1}

betas = 0.04(Vm+12)/exp[(Vm+12)/10]-1}

alphar = 2/exp[(Vm+94)/10]

betar = 8/{exp[(Vm-68)/-27]+1}

Nernst coefficient was calculated for a temperature of 35° C, and external calcium concentration was set to 1.2mM.
 

K_C channel:

IC = gCc2d(Vm-EK)

EK = -85 mV

alphac = -0.0077(Vm+Vshift+103)/{exp[(Vm+ Vshift +103)/-12]-1}

betac = 1.7/exp[(Vm+Vshift+237)/30]

Vshift = 40Log([Ca,1]in)-105

tauc = 1.1 ms

alphad = 1/exp[(Vm+79)/10]

betad = 4/{exp[(Vm-82)/-27]+1}
 

K_AHP channel:

IAHP = gAHPq(Vm-EK)

EK = -85 mV

alphaq = 0.0048/exp[(10Log([Ca,2]in-35)/-2]

betaq = 0.012/exp[(10Log([Ca,2]in+100)/5]

tauq = 48 ms
 

K_M channel:

IM =gMu2(Vm-EK)

EK = -85 mV

alphau = 0.016/exp[(Vm+52.7)/-23]

betau = 0.016/exp[(Vm+52.7)/18.8]
 

K_A channel:

IA =gAab(Vm-EK)

EK = -85 mV

alphaa = -0.05(Vm+20)/{exp[(Vm+20)/-15]-1}

betaa = 0.1(Vm+10)/{exp[(Vm+10)/8]-1}

alphab = 0.00015/exp[(Vm+18)/15]

betab = 0.06/{exp[(Vm+73)/-12]+1}
 

K_Ap channel (see additional notes):

IAp =gApa4b(Vm-EK)

EK = -85 mV

ainf = 1/{exp[(-Vm-5)/10]+1}

taua = 0.15ms

binf = 1/{exp[(Vm+56)/8]+1}

taub = 5ms if Vm<-30 mV and 5+0.26(Vm+30) if Vm>30 mV
 

K_Ad channel (see additional notes):

IAd =gAda4b(Vm-EK)

EK = -85 mV

ainf = 1/{exp[(-Vm-15)/8]+1}

taua = 0.15ms

binf = 1/{exp[(Vm+56)/8]+1}

taub = 5ms if Vm<-30 mV and 5+0.26(Vm+30) if Vm>30 mV
 

K_DR channel:

IDR =gDRn4(Vm-EK)

EK = -85mV

alphan = (-0.018Vm)/[exp(Vm/-25)-1]

betan = 0.0036(Vm-10)/{exp[(Vm-10)/12]-1}
 
 

2. Axon channels:

In the axon, Na+ channels were identical as for the somatodendritic membrane, while the DR-type K+ channel was obtained from Traub et al. (1994):
 

K_DRA channel:

IDRA =gRTAnax4(Vm-EK)

EK = -85mV

alphan(ax)= -0.03(Vm+47.8)/{exp[(Vm+47.8)/-5]-1}

betan(ax) = 0.45exp[(Vm+53.0)/-40]
 
 

3. Ca dynamics:

As described by Warman et al. (1994) and Borg-Graham (1998), the [Ca]i was simulated with two different Ca pools with different time constants, tau1 = 0.9 ms for the calculation of ECa and modulating the C-type K+ current and tau2 = 1 s for the AHP-type K+ current, as follows:
 
 



Where taui is the i-th calcium pool removal time constant, fi is the fraction of Ca influx affecting the i-th pool (f1=0.7, f2=0.024), w is the diffusion thickness (1 micron), A is the compartment area, z is the valence of the calcium ion and F is Faraday's constant.
 

4. Additional notes:

For the neuron prototype 4 in Figure 7 and also in figures 9 (Ortho-1, Anti), 10 (Anti-ctrl, Anti-cond) and in figure 9 (Ortho-2) we used an A-type K+channel modified from Hoffman et al (1997) with a different description for proximal and distal dendrites (K_Ap and K_Ad as defined above).

Since the objective of this work is to simultaneously reproduce both AP parameters and the aggregate PS profile, the channel distributions along the cell morphology have been continuously tuned in a feed-back manner. The detailed distribution of channels along the morphology can be obtained from the neuron scripts.
 
 

  1. Stimuli simulation: 
Simulation of antidromic stimulation was made by 1 nA, 0.1 ms long pulses injected in the Ranvier node (compartment named 'r3' in the neuron scripts) of each cell in the population. We used a binomial distribution to set the activation time for each neuron in the assembly in order to simulate the temporal jitter. Synaptic activation was simulated with alpha functions as follows: gsyn(t) =(t/tausyn){exp(1-t/tausyn)}. The synaptic currents are defined as Isyn = gsyn(t)(Vm-Esyn), with tausyn of 2, 7, and 30 ms and reversal potentials of 0, -75, and -85 mV, for AMPA, GABAA and GABAB mediated currents, respectively. GABAA currents were distributed in the soma and proximal apical shaft, and turned on 1.5 ms after antidromic activation, while GABAB currents were distributed throughout most of the apical tree and activated along with the former, both 1.5 ms after AMPA-type currents initiation, for orthodromic activation. See neuron scripts for the detailed description of the distribution of the synapses.
     
     
  1. Computational methods: 
Compartimental transmembrane currents were calculated using the GENESIS simulator (Bower and Beeman, 1998). Calculations of Field potentials and CSDs were programmed in dedicated C code.
     
     
  1. Bibliography: