
Manuel Alfonseca, Juan de Lara, Estrella Pulido
Universidad Autonoma de Madrid, Dept. Ingenieria Informatica
{Juan.Lara, Manuel.Alfonseca, Estrella.Pulido}@ii.uam.es
Acknowledgement: This paper has been sponsored by the Spanish Interdepartmental Commission of Science and Technology (CICYT), project numbers TIC-96-0723-C02-01 and TEL97-0306.
This paper describes a language designed to write and generate object-oriented simulation code. The language is called OOCSMP, an object-oriented extension of the CSMP simulation language, also extended to solve partial differential equations using different methods. Programs are automatically translated into C++ and JAVA. Graphical user interfaces are automatically generated for various operating systems. The procedure is demonstrated by the implementation of models of gravitation as applied to the solar system and different satellite systems.
System simulation [1] is one of the oldest areas of computer science, well advanced in the sixties, that came to maturity in the seventies. There are two major branches: continuous and discrete simulation. In this paper, we are focusing on the former.
Continuous simulation has usually been programmed either in a special purpose language, or in general purpose code. Continuous simulation languages may be of different kinds, depending on their syntax:
Object-oriented programming originated in the sixties in a discrete simulation language, SIMULA67 [7], which incorporated many of the ideas later included by Alan Kay in the first general purpose object-oriented language, Smalltalk [8], and by Bjarne Stroustrup in C++ [9]. Object-oriented continuous simulation languages and tools, however, took longer to arrive. Object orientation has been added to continuous simulation in two different ways:
In a previous paper [12], we proposed some extensions to the CSMP language to support some object-oriented constructions. These extensions have now been considerably improved, and the OOCSMP language capabilities have been substantially enhanced with the ability to solve partial differential equations.
The OOCSMP language is a true extension of the old CSMP simulation language, in the sense that CSMP programs can still be compiled and executed by our compilers. The extensions added to the language make it possible to build extremely compact object-oriented models when the system to be simulated consists of many similar interactuating parts, as in the gravitational examples we present here and others we have developed. These extensions have now been considerably improved, and the OOCSMP language capabilities have been substantially enhanced with the ability to solve partial differential equations (PDE's). PDE's can be solved by different methods such as the finite elements method and the finite differences method that can be mixed to solve a specific equation. The language also implements an algebra for matrices and vectors. All this adds greatly to the power of the language and extends its domain of application.
Several extensions have been introduced to CSMP to define object-oriented models. These extensions make it possible:
CLASS class-name [: parent-class] {
data declaration section
[INITIAL section]
DYNAMIC [argument-list]
dynamic section
[method-name [argument-list]
method-body]
[directive section]
}
class-name object-name ( [list-of-attribute-values] )
class-name collection-name := object-list
INCLUDE file-name
object-name.attribute
object-name.method([argument-list])
variable += expression
variable -= expression
indicating that the value of the expression is to be added to (subtracted
from) the current value of the variable.
Listing 1 gives an example of the declaration of a class.
*********************************
* Definition of Planet class *
*********************************
CLASS Planet {
NAME name
DATA M, X0, Y0, XP0, YP0, FI
INITIAL
FIR:=FI*PI/180
CFI:=COS(FIR)
SFI:=SIN(FIR)
*********************************
* Calculations for a planet *
*********************************
DYNAMIC
* Distance to the Sun
R2 := X*X+Y*Y
R := SQRT(R2)
Y1 := Y*CFI
Z := Y*SFI
* Mutual influences
* The Sun on this planet
APS := G*MS/R2/R
* This planet on the Sun
ASP := G*M/R2/R
XPP := -(ASP+APS)*X
YPP := -(ASP+APS)*Y
XP := INTGRL(XP0,XPP)
YP := INTGRL(YP0,YPP)
X := INTGRL(X0,XP)
Y := INTGRL(Y0,YP)
*********************************
* Mutual actions of two planets *
*********************************
ACTION
* Distance to another planet
DPP2 := (Planet.X-X)*(Planet.X-X)+(Planet.Y-Y)*(Planet.Y-Y)+(Planet.Z-Z)*(Planet.Z-Z)
DPP := SQRT(DPP2)
* Influences
* The other planet on the Sun
ASP1 := G*Planet.M/Planet.R2/Planet.R
* The other planet on this planet
APP1 := G*Planet.M/DPP2/DPP
* Coordinate conversion
Y2 := Planet.Y*COS(Planet.FIR-FIR)
* Actual action of the planet
XPP += APP1*(Planet.X-X) - ASP1*Planet.X
YPP += APP1*(Y2-Y) - ASP1*Y2
*********************************
* Other data *
*********************************
PRINT R
PLOT Y,X
FINISH R=.0001
}
Listing 1: Declaration of a class in OOCSMP
Listing 2 gives an example of the construction of several objects of class Planet, assuming that the definition of this class is contained in file "Planet.csm".
*********************************
* Universal data *
*********************************
DATA G:=0.00011869, PI:=3.141592653589793
* Sun mass
DATA MS:=332999
INCLUDE "Planet.csm"
*********************************
* Actual planets *
*********************************
Planet Mercury("Mercu",0.055271,-0.3871, 0, 2.078, -9.892, 7.004)
Planet Venus ("Venus",0.81476, 0.7233, 0, 0.051, 7.39, 3.394)
Planet Earth ("Earth",1, 0, 1, -6.2899, 0.107, 0 )
Planet Moon ("Moon", 0.01235, 0, 0.9975,-6.0783, 0.107, 0 )
Planet Mars ("Mars", 0.10734, 1.5233, 0, 0.476, 5.071, 1.85 )
Planet Apollo ("Apolo",1957E-14, 0, 1.4849,-4.253, 2.915, 6.4 )
Planet Jupiter("Jupit",317.94, 0, -5.2028, 2.754, 0.131, 1.308)
Planet Saturn ("Satur", 95.181, 9.5388, 0, 0.113, 2.034, 2.488)
Planet Uranus ("Urano", 14.535, 0, 19.1914,-1.431, 0.067, 0.774)
Planet Neptune("Neptu", 17.135,-30.0611, 0, 0.0117,-1.147, 1.774)
Planet Pluto ("Pluto",0.0021586,0, -39.5294, 0.971 , 0.249,17.148)
Planet System := Mercury, Venus, Earth, Moon, Mars, Apollo, Jupiter, Saturn, Uranus, Neptune, Pluto
System.STEP()
System.ACTION(System)
**********************************
* Time intervals and other data *
**********************************
TIMER delta:=.0005, FINTIM:=2, PRdelta:=.1, PLdelta:=.01
METHOD ADAMS
Listing 2: Simulating the solar system in OOCSMP
A geo-stationary satellite which keeps constant its distance to the Earth has been simulated using the Planet class above-defined without any change.
**********************************
* Universal data *
**********************************
DATA G:=4.979E-16, PI:=3.141592653589793
* Earth data
DATA MS:=5.979E21
INCLUDE "Planet.csm"
**********************************
* Actual satellites *
**********************************
Planet Geost ("Geost",1, 0, 42.24637, -265.462, 0, 0 )
Planet Moon ("Moon", 7.384E19, 0, 392.1, -86.65, 4.4, 0 )
Planet System := Geost, Moon
System.STEP()
System.ACTION(System)
**********************************
* Time intervals and other data *
**********************************
TIMER delta:=.0005, FINTIM:=2, PRdelta:=.1, PLdelta:=.01
PRINT Geost.X
METHOD ADAMS
Listing 3: Simulating a geostationary satellite
The universal data have been computed using a different set of physical units. Variable MS becomes in this case the mass of the Earth, expressed in those units (megagrams, or metric tons). The effect of the Moon on the satellite's orbit is illustrated by performing a double simulation in the presence and in the absence of the Moon. To test the second case, we only have to change the mass of the Moon to zero.
A new block (PDE) has been added to the set of predefined CSMP blocks to make it possible to solve partial differential equations of the form:
A(x,y,...)*U:sub.xx:esub.+B(x,y,...)*U:sub.xy:esub.+C(x,y,...)*U:sub.yy:esub.+D(x,y,...)*U:sub.x:esub.+
E(x,y,...)*U:sub.y:esub.+F(x,y,...)*U+G(x,y,...)=0
where U:sub.x:esub. is the partial derivative of U with respect to
variable x, U:sub.xy:esub. is the second partial derivative of U with respect
to variables x and y, and A,...,G are expressions, which may be functions of
TIME and/or any other model variable. Obviously, if a function is zero, the
corresponding term in the equation vanishes. The equation is solved using the
method of finite differences.
The syntax of the PDE block is as follows:
P:=PDE(Minit, Mderiv-1, Mderiv-2,
VAR-1, VAR-2, A,B,C,D,E,F,G[,x:sub.0:esub.,y:sub.0:esub.])
Where Minit is a matrix of dimensions equal to those of the grid, where the boundary or initial conditions have been previously set, and where the computed values will be filled by the execution of the PDE block. Mderiv-1 and Mderiv-2 are matrices of the same dimensions as Minit, where the derivative conditions with respect to the first variable (and to the second one) are set. Var-1 and Var-2 are the derivative variables. One of them can be the time. A,...G are the expressions that multiply the derivatives of the unknown function. If Var-1 and Var-2 are spatial variables, then the last two arguments of the block (x:sub.0:esub., y:sub.0:esub.) are optional and provide the coordinates of the lower left corner of the grid, their default values being zero. On the contrary, if Var-1 is the time, x:sub.0:esub. represents the initial time.
For example, let us assume that we want to solve the Heat equation in 1-D:
U:sub.t:esub.-K*U:sub.xx:esub.=0
We want to solve the equation for two connected bars, with a length of 2m, and a different coefficient K. In this case, the variable Var-1 will correspond to TIME and Var-2 to x. Expression C will take the value 1, and expresion D, the value -K. We can model a class named Bar, and encapsulate the equation in it. Then, we will connect them, setting the boundary conditions of the second bar as the value of the heat of the first bar at the right end. The OOCSMP program would be:
CLASS Bar
{
NAME name
* Res[;] -> it stores the result of the PDE
DATA Initial[20], Res[200;20], K := 4.8
*****************************************
* This function has four parameters: the
* first two are the vectors containing
* the initial and boundary conditions.
* The last two correspond to the initial
* time and the initial value for x
****************************************
DYNAMIC A[], B[], Tinit, Xinit
* We copy the initial and boundary
* conditions that can vary with
* time
Res[0;] := Initial
Res[;0] := A
Res[;19]:= B
* Heat Equation in 1-D : (d/dt)u-K*(d2/dxx)u = 0
PDE (Res ,0 ,0 ,TIME ,X, 0, 0, -K, 1, 0, 0, 0 ,Tinit ,Xinit )
}
DATA A1[20], A2[200], A3[200], A1[i]=0, A2[i]=10, A3[i]=0
Bar b1("bl",4.4)
Bar b2("b2",4.1)
INITIAL
XInit1 := 20*Xdelta
****************************************
* main section
****************************************
b1.STEP ( A2, b2.Res[;1], 0, 0)
b2.STEP ( b1.Res[;18], A3, 0, XInit1 )
TIMER Xdelta:=0.1, Ydelta:=0.001, delta:=0.0005, FINTIM:= 0.21
PLOT b1.Res
Listing 4: Resolution of a partial differential equation
As it can be seen, the generated interface makes it possible to change the value of the parameters for each bar at simulation time and experiment with the changes.
Figure 1 shows the solution of the equation for the second bar.

Figure 1: Solution of differential equation
Another example we have tested is taken from Y.Chu [13], where it was programmed in Mimic. It models the control system for a three-axis-oriented telescope mounted onto an orbiting spacecraft. We have translated the model into OOCSMP and used two additional constructions of the language to simplify its use. These constructions are:
The model can be tested at the following web address: http://www.ii.uam.es/~jlara/oocsmp/satellit.html
We have built a compiler that translates OOCSMP models into C++ and/or Java. Graphical user interfaces may also be automatically generated for DOS, Amulet [14] (an object-oriented prototype-instance interface developed by Carnegie-Mellon University), and Java. Thus, a single compiler may generate models that work in very different environments, such as Unix, MacOS, Windows-95 and DOS. The compiler allows to choose between four different graphical outputs: bidimensional-plots, three-dimensional plots and two types of iconic representations. Different environments can be used for parameter adjustment and it is also possible to provide several versions of the same model that can be selected by means of buttons. Depending on the compiling options used, we can tailor the compiler to:
To debug the models, we usually start by generating C++ code, provided with a graphic interface that makes it very easy to adjust the values of the different parameters in the system and shows the results of the simulations as graphical plots.
Once debugged and adjusted, the same compiler, invoked with different options, can be used to generate Java applets and html skeletons. The same model, with a few adjustments, may be used to simulate different gravitational systems, and thus generate the several html pages that make up the course.
In addition, we have developed a procedure to semiautomatically generate Internet educational courses based on simulation. It consists of the following steps:
Manual adjustment are needed to fill the html skeletons with explanations, images and cross references to other pages. The resulting set of pages is ready to be made available to the students through the Internet. (See the gravitational simulation at http://www.ii.uam.es/~epulido/newton/grav.htm). Figures 2 and 3 show the appearance of some of the pages.
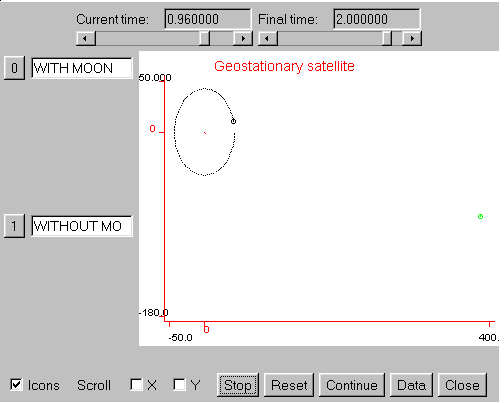
Figure 2: A geostationary satellite
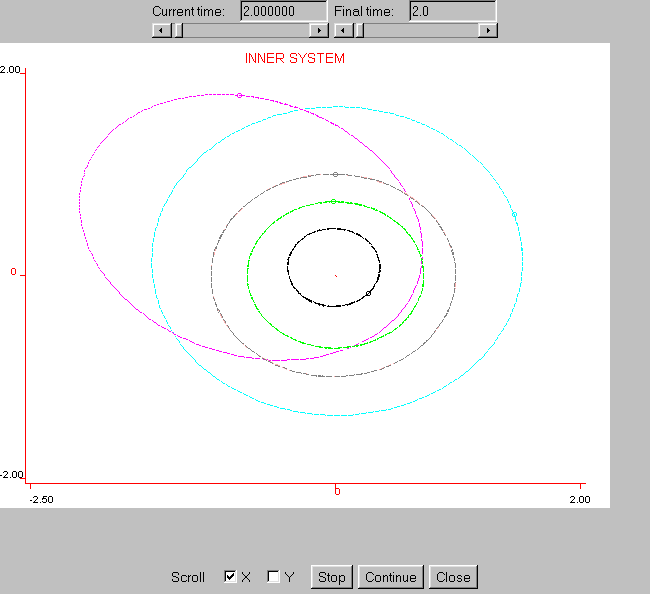
Figure 3: Gravitational simulation
As the examples make clear, the OOCSMP language makes it possible to build extremely compact and reusable object-oriented models when the system to be simulated consists of many similar interactuating parts. The ability to solve a large family of partial differential equations also adds greatly to the power of the language and extends its domain of application.
The automatic generation of html and Java code makes it very easy to develop courses for the Internet based on continuous simulation. We have applied the procedure to three different application areas: simulation of Newton's laws, ecological systems [15], and electronic circuits [16].
In the future, we intend to extend the language to different families of partial differential equations, such as those including time derivatives of one or more variables.